日常の感覚ではありえないにも関わらず数学的には存在するものがある。
ここでは数学の進展に寄与した連続写像の例を紹介しよう。

１．空間充填曲線：「次元」の数学的定義の必要性を導いた連続写像

「次元」は「次元は空間の広がりを表す一つの指標」と理解されている素朴で直感的な数学的概念の一つである。座標空間では座標の数を、また図形に対してはそれを表示するパラメータの数を次元と呼ぶことが多い。ベクトル空間の次元は「基底の数」で定義している。これは前者の立場を表している。また平面上の円などの2次曲線は上手にパラメータ表示をすることで一つの変数で表示することができる。そして、直線、正方形、立方体の次元がそれぞれ1, 2, 3であることはほとんど疑うことなく受け入れられているであろう。数学では事象を記述する座標の数が次元になるので高次元空間や無限次元空間も存在し、それらを研究する幾何学も存在する。

一方、物理学では物理量の自由度と捉える立場が一般的で、物理現象を捉える物理的単位の数で記述している。そのため、数学とは異なる意味合いである。ドラえもんの四次元ポケットは（作者が意味の違いを考えていたか分からないが）物理の意味の次元で考えていたのだろう。

ここでは、数学、位相幾何学の立場で考えてみよう。E. Netto (1879) は単位閉区間 [0, 1] から正方形 [0, 1]2 の上への連続な全単射が存在しないことを示した。それでは、全単射という条件がなければ、すなわち、単位閉区間から正方形への連続な全射が存在するかという疑問が生じた。それは、私たちが単位閉区間 [0, 1]からユークリッド平面への連続写像の像を平面曲線、3次元ユークリッド空間への連続写像の像を空間曲線と呼ぶなかで、面積をもたない直線から面積をもつ領域、例えば正方形 [0, 1]2のすべてを通るような曲線が存在するか？　という問題と同等である。この問題はG. Peano (1890) がそのような曲線の存在を示し、解決した。以下の図はD. Hilbert (1891)によるその幾何的な生成手続きを示したものである：[0, 1]からの連続写像の列 f1, f2, f3, ….を図のように定め、その極限として求める連続な全射 f : [0, 1] → [0, 1]² を定めている。このような曲線を空間充填曲線と呼ぶ。


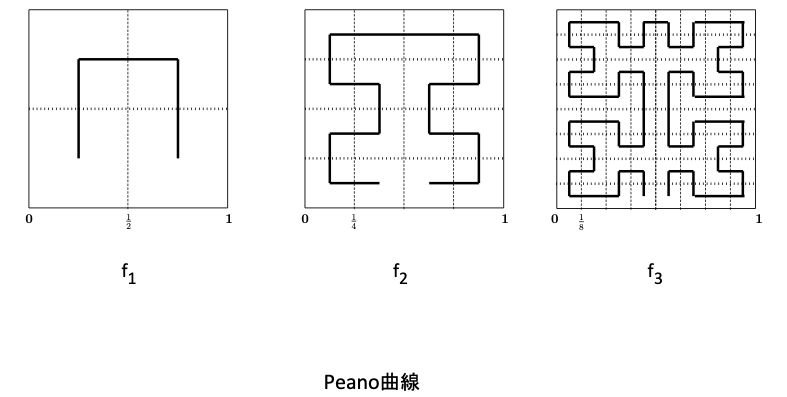
しかし、この問題の解決が「次元の概念の数学的定義を確立」という新たな問題を生じさせ、位相幾何学の初期の発展をもたらした。この流れで1913年に L.E.J. BrouwerがH. Poincaréのアイディアに基づき大きな帰納的次元 Ind Xの定義を与え、小さな帰納的次元 ind XやLebesgue-Čechによる被覆次元 dim X の定義へ進展した。今、私たちはこれら三つの定義を適宜使い分けて利用している。

２．Cantor関数：線分を0次元空間からの連続写像で埋め尽くす

次元の定義が確立すると、点が離散にある状況を連結成分のあり方で表し、0次元空間を捉えることができた。直線、正方形、立方体がそれぞれ1, 2, 3次元空間のモデルであるように0次元空間のモデル「カントール集合C」を、次のように閉区間を3等分して真ん中の開区間を次々に取り除いて得られるCnの共通部分として得ることができた。


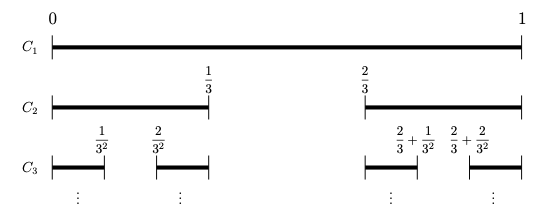
さらに、このカントール集合Cから [0, 1]への連続写像を定義することができる。直感的には、取り除いた開区間 (1/3, 2/3)を 1/2へ、(1/9, 2/9)を 1/4,(7/9,　8/9)を3/4へ写すという下図のような連続写像を考えている。


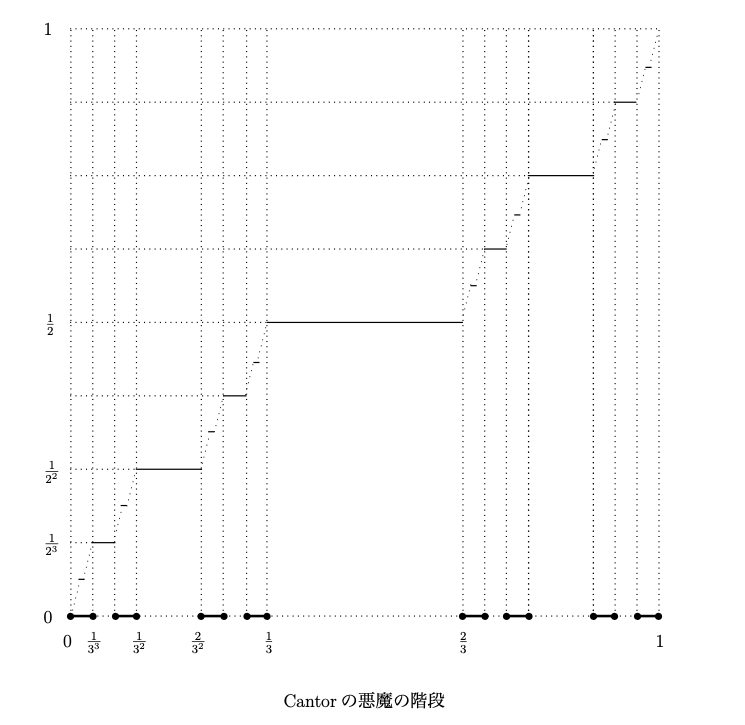
奇妙な形をしているこのグラフは「カントールの悪魔の階段」と呼ばれている。[0, 1]上の連続写像 y=f(x) いたる所で微分係数が0ならば f(x)は定数になる。しかし、この写像は、確率1で平坦であるにもかかわらず、0から1へ増加している不思議な連続写像である。

３．応用数学へ

近年のコンピューター技術の急速な進歩に伴って、日常の感覚ではありえない無限回操作による数学の対象がかなり視覚化されるようになった。実際、エレガントな再帰構成を行うことで様々な空間充填曲線を描くことができるので、空間充填曲線はプログラミングの教科書によく取り入れられている。これらの曲線を描くための高速計算法の研究は、巡回セールスマン問題への応用など対象数が多くなった場合の高速近似法に有効である。

今回取り上げた例だけでなく、不思議な数学は数多くある。その不思議さを味方に付け、新しい応用数学を発見していくことは魅力的な方向づけになると予想されている。