輪郭線の幾何学

私の専門は幾何学，特に特異点論と特性類理論を研究しています．本稿では，身近な絵画や写真に現れる《輪郭線》を題材に，そのトポロジー（位相幾何学）についてお話します．

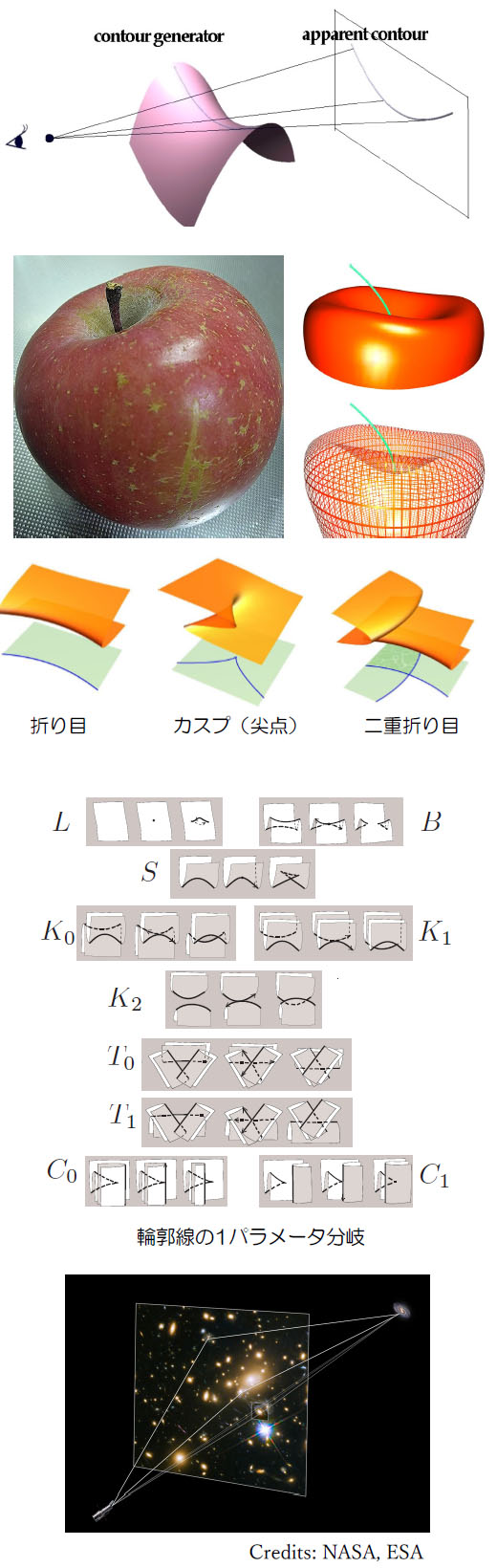
物の輪郭を描くことは，自分の周りの世界を描き写す根源的な所作です．少し数学的な設定で言えば，空間内の滑らかな曲面をある視点から平面（キャンバス）に射影することを考えます．視線（視点とキャンバス上の点を結ぶ直線）と曲面との接点の軌跡を輪郭母線と呼び，その射影像であるキャンバス上の平面曲線を輪郭線と呼びます．ホイットニーの定理によれば，曲面の射影の局所的形状は，視点が一般的な位置にあれば，折り目・カスプ・二重折り目の３種類あります．約２万年前に描かれたラスコー洞窟の馬の壁画にも，この輪郭線の特徴の片鱗が見て取れるでしょう．

折り目は，断面をとれば高校の微積分で習う１変数関数の極大・極小値に対応します．つまり，２階微分で決まる現象です．二重折り目は，同一の視線に対して曲面の異なる２箇所で折り目を生じる点です．ではカスプとは何でしょうか．図にあるリンゴの写真において，目を凝らしてリンゴのくぼみ付近手前の輪郭を見れば，事実，輪郭が先に伸びていません！リンゴを透明な曲面にすれば，実は輪郭母線は途切れることなく曲面上の滑らかな曲線であって，その像である輪郭線は尖った形状になります．この尖った点での速度ベクトルは０であり，輪郭母線が視線と接することを意味します．これがカスプであって，３階微分が関わる現象です．日常，辺りを見回せば，３次の現象が至る所にあるのですね．　

折り目・カスプ・二重折り目は少し視点を動かしても本質的に変わらず安定しています．では，視点を連続的に動かして大きく変化させたらどうでしょうか．すると，ある時刻の前後で輪郭線の形状も変わり，一般に下図のような１０種類の局所的な分岐が現れます．たとえばSタイプは４次の現象を反映するものです． いま，視点が空間曲線Cに沿って動く際，その射影にこれらの局所分岐が何度か繰り返し起きて，輪郭線の大域的な形状が変化したとしましょう．１０種類の各タイプについて，左から右に変化したら＋１，その逆は−１と勘定します．たとえばLタイプであれば，この±１の総和をΔLで表します．この表記を使えば，輪郭線のカスプの個数の増加分および二重折り目の個数の増加分は各々

2(ΔL +ΔB +ΔS )，

ΔS + 2(ΔK₀ +ΔK₁ +ΔK₂ +ΔC₀ +ΔC₁ )

と書けますね（各自確かめよ）．端点を止めて曲線Cをどのように取ってもこの量は変わりません．実は，このような「局所変形で記述できるが曲線Cの取り方に依らないで始点と終点だけで決まる量」はもう一種類あって，それは

ΔL +ΔB +2(ΔK₀ –ΔK₁ +ΔK₂ )

です．これは全く非自明であって，平面フロントのサーストン・ベネクィン不変量と呼ばれるものに対応します．応用分野のコンピュータ・ヴィジョンでも取り上げられています．

このような輪郭線の幾何学に関して，その代数幾何版は《数え上げ幾何学》の範疇に入りますし，曲面や輪郭線の曲率に関する微分幾何学の話題も多く成されています．天文学への応用もあります．１００億光年以上離れた銀河が発する光はダークマターによる重力場レンズ効果で捻じ曲げられて，ハッブルあるいはジェームス・ウェッブ望遠鏡のスクリーンに投影されます．例えば，「遠い一つの銀河はスクリーン上では奇数個の像として観測される」という定理があります．この場合，輪郭線自体は見えませんが，銀河の像達の振る舞いに輪郭線の幾何学が関わります．

物の輪郭を描くと言っても，その数理は斯様に多様であって奥深いものなのです．