モジュライ空間とミラー対称性

「数学とは異なるものを同じと見做す技術である」とはフランスの数学者ポアンカレの言葉です。みかんが1個、みかんが2個、みかんが3個…, 腕を1回転、腕を2回転、腕を3回転…, コーヒーを1口、 コーヒーを2口、コーヒーを3口…, これらは本質的に異なる事物や動作ですが、適切な視点からは同じと見なすことができます。つまり数として捉えられます。またドーナツとマグカップが数学者には同じに見えるという話も有名ですが、これはトポロジー(位相幾何学)の考え方の一例です。

一方で、同じような数学的対象の「異なり具合」を認識することも重要です。調べたい対象に対して、その仲間を全て集めて、全体でどのような構造をしているのかを数学者はしばしば考えます。このとき、考察対象を分類するパラメータ空間はモジュライ空間と呼ばれます。

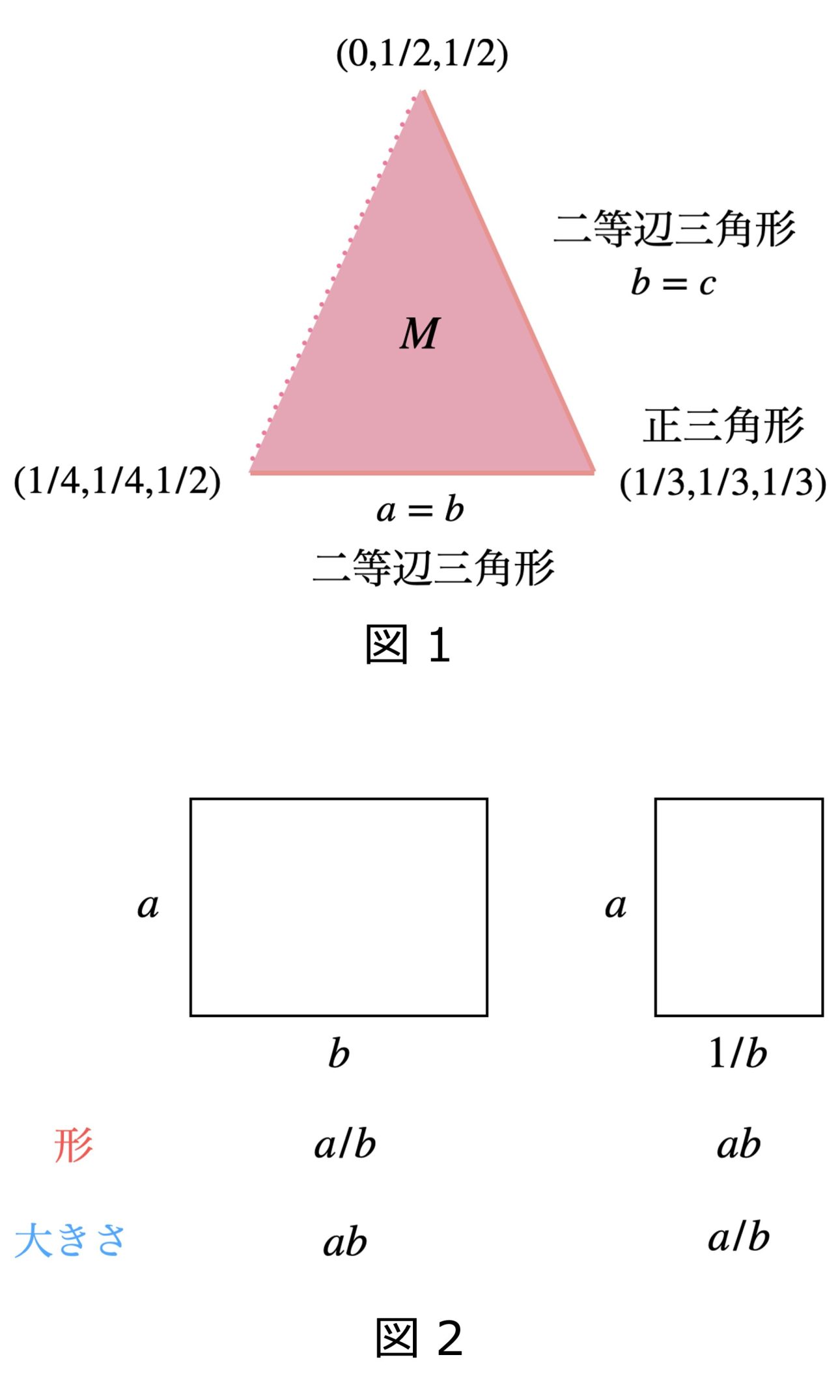
例として、三角形のモジュライ空間\(M\)を考えてみましょう。ただし二つの三角形は互いに相似の関係にある場合に同じと見なすことにします。三辺の長さを\(a,b,c\)として、\(a \le b \le c\)なる大小関係を課しても一般性を失いません。また拡大縮小しても同じ三角形と考えるので、三辺の和は1とします。このとき三辺の長さ\(a,b,c\)の三角形が存在するための必要十分条件は三角不等式\(a+b > c\)で与えられます。これよりモジュライ空間\(M\)は3次元ユークリッド空間\(\mathbb{R}^3\)のある2次部分集合となることがわかります。(図1)

実際、どの三角形も\(M\)のある点\((a,b,c)\)から定まる三角形と相似であり、\(M\)の相異なる2点から定まる三角形は互いに相似にはなりません。\(M\)自身は三角形から一辺を除いた空間となり、\(M\)の境界は二等辺三角形に対応します。一般に、モジュライ空間はそれが分類する対象の構造を反映しており、モジュライ空間を解析することで考察対象のより深い情報を取り出すことが可能となります。

次に長方形のモジュライ空間を考えましょう。ただし上下左右の方向は固定し、相似でも大きさの異なる長方形は異なるものとします。このような長方形は形と大きさの二つのパラメータで分類されます。つまり、高さが\(a\)、底辺の長さが\(b\)の長方形に対して、その形は高さと底辺の長さの比\(a/b\)、大きさは高さと底辺の長さの積\(ab\)で与えられます。また形と大きさが同じであれば、同じ長方形であることもすぐわかります。

実は、長方形には双子の相手がいることが知られています。高さが\(a\)、底辺の長さが\(b\)の長方形\(X\)の相手は、高さが\(a\)、底辺の長さが\(1/b\)の長方形\(Y\)です。長方形\(Y\)の形は\(ab\)、大きさは\(a/b\)となるので、\(X\)と\(Y\)の間に形と大きさを入れ替える双対性が見てとれます。(図2) 人間で例えれば、身長と体重が互いに逆となる人間\(X\)と\(Y\)が常に存在するようなものです。

私は主にカラビ・ヤウ多様体と呼ばれる高次元の曲がった空間に興味があります。カラビ・ヤウ多様体に対しては、複素構造とシンプレクティック構造の二つのモジュライ空間を考えることができます。大雑把に言えば、前者はカラビ・ヤウ多様体の形に、後者は大きさに対応します。カラビ・ヤウ多様体は沢山存在しますが、長方形のように、双子の相手が常に存在すると信じられています。この予想はミラー対称性と呼ばれ、超弦理論の研究で見つかった現象です。実は上述の長方形の双対性の例は楕円曲線と呼ばれる一番簡単なカラビ・ヤウ多様体のミラー対称性の実部を切り出したものです。

ミラー対称性は豊富な予想群を数学にもたらし、新分野を切り開く大きな推進力となってきました。この双対性はフーリエ変換の幾何学化とも考えられ、様々な分野を有機的に繋げ、幅広い応用があると期待されています。