近年，人工知能で着目されている機械学習技術は，あるモデルに基づきデータを用いて何かを機械的に学習する技術です．その「何か」は，そのモデルが対象とする問題に応じて様々ですが，例えば，サンプルデータの近似直線を求める問題では，その直線の傾きにあたります．ここではその「何か」を「パラメータ」と呼ぶことにしましょう．

様々な機械学習技術の中で，近年特に著しい発展を遂げているアプローチは，目的関数を定義し（先の例ではサンプルデータと直線の距離），与えられた制約条件の下でその目的関数を最小（または最大）にする「最適化問題」を定義して，パラメータ（傾き）を求解するものです．その観点で

“機械的に学習すること（機械学習） ≒ 最適化問題を解くこと”

と言うことができます．実際，Goolge社やAmazon社などがしのぎを削る機械学習分野の最難関トップ会議NeurIPSやICMLで発表される研究論文の多くは，最適化モデルや求解手法，あるいはそれらと密接に関連しています．

ところで，パラメータが探索領域Mの中で連続的に変化する連続最適化問題の求解手法は，パラメータに「制約条件」がない手法と制約条件がある手法に分けられます．前者は目的関数やその微分の情報等を用いますが，後者は制約条件も考慮するので複雑です．ところが，探索領域M自体の内在的な性質に注目すると，制約あり問題をM上の制約なし問題とみなすことができます．特にMが幾何学的に扱いやすい「リーマン多様体」のとき，その幾何学的性質を利用して，ユークリッド空間上の制約なし手法をリーマン多様体上に拡張した手法を用います．リーマン多様体とは，局所的にはユークリッド空間とみなせるような曲がった空間で，各点で距離が定義されています．また制約条件には，列直交行列や正定値対称行列，固定ランク行列など，線形代数で学ぶ行列が含まれます．このアプローチは「リーマン多様体上の最適化」と呼ばれますが，実際，この手法が対象とする問題は，前述の制約条件が現れる様々な応用に適用可能です．例えば，主成分分析等のデータ解析や，映画や書籍の推薦，医療画像解析，異常映像解析，ロボットアーム制御，量子状態推定など多彩です．深層学習における勾配情報の計算の安定性向上の手法としても注目されています．

一般に，連続最適化問題で用いられる反復勾配法は，ある初期点から開始し，現在の点から勾配情報を用いた探索方向により定まる半直線に沿って点を更新していくことで最適解に到達することを試みます．一方，リーマン多様体Mは，一般に曲がっているので，現在の点で初速度ベクトルが探索方向と一定するような「測地線」と呼ばれる曲がった直線を考えて，それに沿って点を更新します．ここで探索方向は，現在の点の接空間（接平面を一般化したもの）上で定義されます．


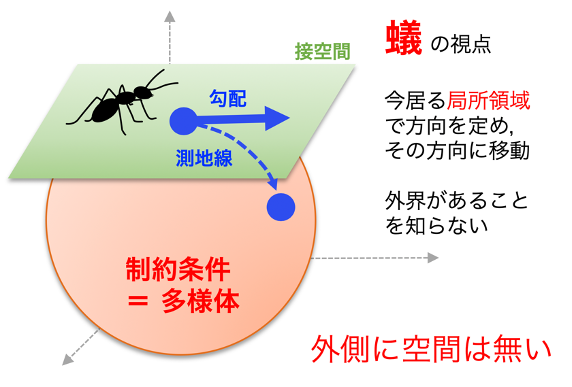
このリーマン多様体上の最適化ですが，古くは例えば1972年の論文まで遡ります．しかし，計算処理上，測地線を求めることは一般的に困難ですので，当時は広く応用されるまでには至りませんでした．当時とは比べものにならないほど計算処理能力が向上した現在においても，扱うデータ数や次元数の増加により，その問題は露わになるばかりです．しかしながら，近年，測地線を近似的に求める様々な手法が研究開発され，様々な問題で著しい成果を上げつつあります．

ところがここでの新たな問題は，ひとたび，点の移動が測地線に沿わなくなったとき，その手法が最適解に収束するかどうかの保証が無くなってしまうことです．最適化の研究では，注目している手法がいかなる初期点から開始しても収束するか，また収束する場合でも，1回の更新処理でどの程度の計算量が必要で，どの程度の更新回数で，どの程度の誤差を含む解まで到達できるか，を理論的に明らかにすることが，主要な研究対象です．さらに，その理論的結果は，その手法を搭載するシステムの設計に直接的に関係するので，応用上も極めて意義がありますし，エンジニアはそこを意識する必要があります．

現在，ユークリッド空間の手法からリーマン多様体上の手法への一般化が主流です．今後は，リーマン多様体上の手法を起源とするユークリッド空間の手法を生み出されること，またこれらの手法が様々な応用に展開されることに期待したいところです．