正20面体を見て美しいと感じる方は多いと思います。数学者はこのような美しい正多面体に興味を持ち、以下の5種類しか存在しないことを発見しました。その後高次元の正多面体の発見・分類へと研究は進んでいきます。



一方1948年、クロード・シャノンは応用数学の新しい分野、符号理論を創始しました。符号理論とは、2つの離れた場所AとBに情報を正しく伝えたい、その効率化などに関する研究です。正多面体と符号理論、この一見異なる分野が、現代では密接に関係することがわかっています。この小文ではこのような古典的な数学的対象と符号理論の関係について見ていきましょう。

「YES、NO」どちらかのメッセージを場所Aから離れた場所Bへ伝える状況を想像しましょう。情報通信ではメッセージを成分が0と1のベクトルに変換し送信します。たとえば「YES → (0)、NO → (1)」のように。しかし通信の途中で誤りが起こって0が1に変換されては困ります。

　　YES → (0) → 誤り → (1) → NO

このように通信途中に誤りが生じると「YES」を送ったつもりが「NO」が届いて、間違ったメッセージが伝わってしまうのです。しかし「YES → (000)、NO → (111)」と変換しメッセージを伝えてみましょう。途中で1つの誤りが生じても

　　YES → (000) → 誤り → (010) → YES

今度は正しくメッセージが伝わっています。なぜなら「(010)」と「(000)、(111)」では「(000)」の方が近く（0と1が異なる箇所がそれぞれ1、2個で、1個の方が近い！）、送ったメッセージは「(000)」つまり「YES」と判断できるのです。しかし途中で2つの誤りが起きたと仮定します。

　　YES → (000) → 誤り → (011) → NO

すると今度は「(011)」は「(111)」の方が近いため、間違ったメッセージが伝わってしまうのです。このような「(000)、(111)」を符号と呼びます。この符号は2つのベクトルから構成されますので、2つの情報を送信でき、さらに上で紹介したことから、1つの誤り訂正能力を持ちます。現実ではメッセージ2つでなく多くの情報を送信する必要があります。さらに多くの誤りを訂正できる符号の発見が重要です。

次をご覧ください。16個の元からなるベクトルですので、16個の情報を送信できます。そして1つの誤りを訂正できる符号です。



たとえば2行目左の「(1101000)」を送信して1つ誤りが生じ、「(1101001)」を受信したとしましょう。このベクトルと一番近いベクトルは送信したベクトル「(1101000)」であることが確認できます。このように多くの情報を送信でき、さらに多くの誤りを訂正できる符号はどのように構成できるでしょうか。ここでぜひ紙と鉛筆（あるいはコンピューター）を用意して16個のベクトルで1つの誤りを訂正できる符号を皆さん作ってみてください。結構難しい問題なのです。

このような符号を構成する方法に正多面体を用いるものがあります。上に掲載した正20面体を取り上げて符号を作ってみましょう。正20面体の頂点は12個存在して、それを \(\it v_i \) (\(\it i\)=1,…,12) と書いたとき，



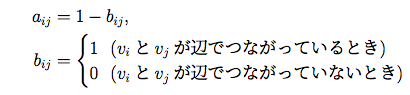
で定義されるベクトル (\(\it a_{i {\rm 1}},…, a_{i {\rm 12}}\)) を12本作りましょう (\(\it i\)=1,…,12)。このベクトル (\(\it a_{i {\rm 1}},…, a_{i {\rm 12}}\)) の左に、次で定義されるベクトル (\(\it d_{i {\rm 1}},…, d_{i {\rm 12}}\)) をつなげます。



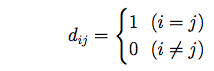
すると次の12本の行からなるベクトルが得られます。



この12本のベクトルを用いて、1行目+2行目、1行目+3行目など、足し算していくと計2048個のベクトルが得られます（1+1=0と考える）。このようにして得られる符号は3個の誤りを訂正できる符号で、ゴレイ符号と呼ばれます。NASAのボイジャー計画で用いられた、大変性能の良い符号が得られるのです。なぜ性能が良いのか、それには正20面体の対称性、美しさが関係しています。

以上、正多面体と符号理論の一つの関係、数学が社会へ役に立つ一つの例を紹介しました。このような数学的に美しいものが、社会に役に立つ現象は多くの応用数学で観察されます。私自身、高次元の正多面体を用いて、優れた性能を持つ符号の系列を発見してきました。このようにこれまで得られた数学の成果を、応用数学の研究へ応用する、あるいは逆に、応用数学の成果を数学へ還元するといった研究を進めております。

参考文献

[1] Mathematica, Wolfram Research, Inc., Mathematica, Version 12.2, Champaign, IL (2020).