ご存じの通り、粒子の運動を表す物理量としての運動量やその保存則である運動量保存則は、大学入試での必須の学習内容と言うこともあり、理工学部の皆様にとって大変馴染み深いものでしょう。では、運動量や運動量保存則は、一体、何を基礎に導かれるのでしょうか。少し不思議な感じがするかも知れませんが、空間が示す対称性の中で、空間の一様性と言う対称性に関係しています。具体的には、一様な空間内での力学的性質は任意の距離の平行移動に対して不変だと言うことです。そこで任意の距離と言うことなので、無限小の平行移動を考えることにより運動量や運動量保存則を導くことができます。また、空間の等方性と言う空間の回転に関係する対称性もあり、無限小回転から角運動量と呼ばれる物理量を得ることもできます。ただ、角運動量については紙面の都合上ここでは触れませんので、興味がある方は各自で調べてみてください。

　物理には、私が専門としている固体（結晶）物理という分野があります。これは結晶中における電子の振る舞いについて、その理解を目的とする学問です。では、固体（結晶）物理の場合でも一様な空間と同様に、電子の運動量を考えて、その振る舞いを理解することは可能なのでしょうか。ここで、一様な空間との相違は、結晶内の電子が周期的な規則正しい原子配列の中を運動していることで、その結果、結晶の持つ対称性からの要請を受けることになります。特に重要な対称性は、周期的な原子配列に関係する有限距離の平行移動の対称性で、このため、結晶中の電子の状態はブロッホの定理と呼ばれる定理を満足しなければなりません。そして興味深いことに、ブロッホの定理を満足する電子の状態に対して、一様な空間で定義される運動量を得ることはできず、また運動量保存則は必ずしも成立しないことが知られています。

　では、結晶中の電子の振る舞いはどのように扱えばよいのでしょうか。実は、結晶内の電子に関しては、結晶運動量および結晶運動量保存則の言う概念を通して、その振る舞いを理解することが可能です。一見、結晶と言う言葉がついているだけのようにも思えますが、一様な空間の場合とは異なるものです。実際、結晶運動量と結晶運動量保存則は数学の離散群の概念と関係していて、このため電子の状態は並進群や空間群と言う対称操作群の既約表現を通して理解されることになります。また、並進群の既約表現が波数ベクトル \(\it k \) で指定されることから、結晶中における電子の振る舞いを理解するには、逆空間や逆格子と言った概念の理解が不可欠です。そこで逆格子を規定する逆格子ベクトルを導入すると、既約表現 \(\it k \) と逆格子ベクトル \(\it g_i \) だけ異なる既約表現 (\(\it k \) + \(\it g_i \)) は同値であることが導かれます。実は、結晶運動量保存則はこの同値性に基づいています。すなわち、繰り返しになりますが、固体（結晶）物理において議論される物理量は、数学における離散群の概念と結びついていて、そこから興味深い概念や物理現象が生まれることになります。例えば、ブリルアンゾーンや電気抵抗でのウムクラップ過程等、固体物理の様々な場面でお目にかかることができます。

　上述したように、固体（結晶）物理では、数学を単に計算手段として利用するのではなく、数学での抽象概念が表現論を通して具現化し、さらに具現化を通して物理現象を理解していくと言う筋道を取ります。しかし、数学、特に線形代数があまり得意ではない学生にとって、分かり難い分野であることも事実です。固体（結晶）物理は不思議な世界です。この小文を通して、多くの学生諸君に少しでも興味を持っていただけたら幸いです。

◎ 材料生産が二酸化炭素を排出する

　世界的に持続可能な開発目標SDGs(Sustainable Development Goals)が掲げられており、中でも地球温暖化に関わる二酸化炭素排出の問題は、世界で知恵を出し合って解決していかなくてはならない課題です。二酸化炭素の問題として発電、すなわち化石燃料（石炭、石油）の大量消費がよくクローズアップされておりますが、我々の生活に不可欠な材料を生み出す過程でも多くの二酸化炭素が排出されます。意外かもしれませんが、二酸化炭素の全分野の内訳において高いものから順に、ものづくり（鉄鋼、セメント、プラスチック）31%、発電27%、移動(飛行機、トラック等)16%と報告されており[1]、素材をつくる過程で最も二酸化炭素が排出されております。鉄鋼材料では鉄鉱石を還元する際に大量の二酸化炭素を発生します。また建築物に多く使われるセメントは、多量の二酸化炭素を固化している石灰石を焼成することで作製され、その際に大量の二酸化炭素が排出されます。輸送機器の軽量化のために多用されているアルミニウムや炭素繊維は、還元や焼成の際に大電力を消費します。材料を生み出す際に、可能な限り省エネルギーでかつ二酸化炭素を排出しないプロセスや新素材の開発が求められております。

◎ 理想的な材料は？

　以上の流れの中で、「天然資源を低エネルギーのプロセスで最高の材料に変換したい」これが一つの材料開発の目標となります。現存する材料の中で軽量でありかつ高強度、高機能である材料は何か、と突き詰めていきますと炭素繊維やカーボンナノチューブに代表される炭素材料に行き着きます。その中でも「グラフェン」は炭素原子1層のナノシートであり、この材料は天然資源である黒鉛をうまく剥がせば取り出せることができます。黒鉛は鉛筆やシャープペンシルに使われているありふれた材料ですが、うまく1枚の原子シートを取り出して活用できれば、今までにない素晴らしい材料が生み出されるものと期待されております。人間の知恵を振り絞ってグラフェンへ剥離する技術ができれば、ありふれた材料をダイヤモンド並みに価値の高いものへ昇華させることができます。

◎ グラフェンの低エネルギー量産化の挑戦

　グラフェンシートはシート同士が弱いファンデルワールス力によって引き付け合い、層状構造の黒鉛となっております。弱い力だから簡単にシートを引きはがせますが、これを原子層レベルまで薄く引き剥がすことは困難であり、また引きはがしたとしてもファンデルワールス力によって再積層するといった問題点があります。黒鉛をグラフェンに低エネルギーで変換する技術は、持続可能な材料開発の観点からも間違いなく重要な研究トピックとなっており、日々新しい手法が報告されております。しかしながら、グラフェン品質と低エネルギー、低コストを両立させる方法はまだ確立されておらず、それゆえ皆さんの周りにもグラフェンで作られた製品は未だ出てきていないのが現状です。ファンデルワールス力に打ち勝ち、再凝集を防ぎつつグラフェンを取り出し、それを応用する道筋を見つけることはとても困難です。しかしながら、困難であるからこそ一連のプロセスが確立された際に大きなインパクトを生み出します。
酸化されたガス化した炭素(CO2)は地球温暖化を引き起こす一因となっておりますが、固化された強固な炭素は、地球を救う材料になるかもしれません。

[1] Bill Gates, How to avoid climate disaster, 2021

正20面体を見て美しいと感じる方は多いと思います。数学者はこのような美しい正多面体に興味を持ち、以下の5種類しか存在しないことを発見しました。その後高次元の正多面体の発見・分類へと研究は進んでいきます。



一方1948年、クロード・シャノンは応用数学の新しい分野、符号理論を創始しました。符号理論とは、2つの離れた場所AとBに情報を正しく伝えたい、その効率化などに関する研究です。正多面体と符号理論、この一見異なる分野が、現代では密接に関係することがわかっています。この小文ではこのような古典的な数学的対象と符号理論の関係について見ていきましょう。

「YES、NO」どちらかのメッセージを場所Aから離れた場所Bへ伝える状況を想像しましょう。情報通信ではメッセージを成分が0と1のベクトルに変換し送信します。たとえば「YES → (0)、NO → (1)」のように。しかし通信の途中で誤りが起こって0が1に変換されては困ります。

　　YES → (0) → 誤り → (1) → NO

このように通信途中に誤りが生じると「YES」を送ったつもりが「NO」が届いて、間違ったメッセージが伝わってしまうのです。しかし「YES → (000)、NO → (111)」と変換しメッセージを伝えてみましょう。途中で1つの誤りが生じても

　　YES → (000) → 誤り → (010) → YES

今度は正しくメッセージが伝わっています。なぜなら「(010)」と「(000)、(111)」では「(000)」の方が近く（0と1が異なる箇所がそれぞれ1、2個で、1個の方が近い！）、送ったメッセージは「(000)」つまり「YES」と判断できるのです。しかし途中で2つの誤りが起きたと仮定します。

　　YES → (000) → 誤り → (011) → NO

すると今度は「(011)」は「(111)」の方が近いため、間違ったメッセージが伝わってしまうのです。このような「(000)、(111)」を符号と呼びます。この符号は2つのベクトルから構成されますので、2つの情報を送信でき、さらに上で紹介したことから、1つの誤り訂正能力を持ちます。現実ではメッセージ2つでなく多くの情報を送信する必要があります。さらに多くの誤りを訂正できる符号の発見が重要です。

次をご覧ください。16個の元からなるベクトルですので、16個の情報を送信できます。そして1つの誤りを訂正できる符号です。



たとえば2行目左の「(1101000)」を送信して1つ誤りが生じ、「(1101001)」を受信したとしましょう。このベクトルと一番近いベクトルは送信したベクトル「(1101000)」であることが確認できます。このように多くの情報を送信でき、さらに多くの誤りを訂正できる符号はどのように構成できるでしょうか。ここでぜひ紙と鉛筆（あるいはコンピューター）を用意して16個のベクトルで1つの誤りを訂正できる符号を皆さん作ってみてください。結構難しい問題なのです。

このような符号を構成する方法に正多面体を用いるものがあります。上に掲載した正20面体を取り上げて符号を作ってみましょう。正20面体の頂点は12個存在して、それを \(\it v_i \) (\(\it i\)=1,…,12) と書いたとき，



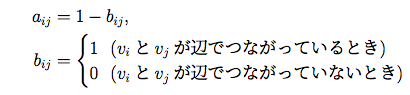
で定義されるベクトル (\(\it a_{i {\rm 1}},…, a_{i {\rm 12}}\)) を12本作りましょう (\(\it i\)=1,…,12)。このベクトル (\(\it a_{i {\rm 1}},…, a_{i {\rm 12}}\)) の左に、次で定義されるベクトル (\(\it d_{i {\rm 1}},…, d_{i {\rm 12}}\)) をつなげます。



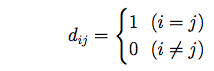
すると次の12本の行からなるベクトルが得られます。



この12本のベクトルを用いて、1行目+2行目、1行目+3行目など、足し算していくと計2048個のベクトルが得られます（1+1=0と考える）。このようにして得られる符号は3個の誤りを訂正できる符号で、ゴレイ符号と呼ばれます。NASAのボイジャー計画で用いられた、大変性能の良い符号が得られるのです。なぜ性能が良いのか、それには正20面体の対称性、美しさが関係しています。

以上、正多面体と符号理論の一つの関係、数学が社会へ役に立つ一つの例を紹介しました。このような数学的に美しいものが、社会に役に立つ現象は多くの応用数学で観察されます。私自身、高次元の正多面体を用いて、優れた性能を持つ符号の系列を発見してきました。このようにこれまで得られた数学の成果を、応用数学の研究へ応用する、あるいは逆に、応用数学の成果を数学へ還元するといった研究を進めております。

参考文献

[1] Mathematica, Wolfram Research, Inc., Mathematica, Version 12.2, Champaign, IL (2020).

さまざまな図形を研究するのが幾何学という学問です．私の研究では，条件を満たす図形の個数を数えるというとても素朴な問題を扱っています．図１を見ると，複雑な曲面の中にいくつかの直線が含まれているのが見えるでしょう．３次式によって定まる曲面という意味で「３次曲面」と呼ばれるものの一つです．一般の３次曲面にはちょうど 27 本の直線が含まれていることが知られています（正確には複素３次元射影空間において３次曲面を考える）．このように，図形（この問題では直線）の個数を数えるという問題を扱う幾何学の一分野を「数え上げ幾何学」と呼んでいます．もう少し広く，図形の集まりを一つの幾何学的な対象として扱うことをモジュライの幾何学と呼びます．数え上げの問題は 0 次元のモジュライを扱っていることになります．

Q：なぜ 0 次元を扱うのですか？
A：理由はいくつも挙げられます．一つには，結果がものの個数，つまり自然数なので，わかりやすくて面白いのです．図２のように，まるでパズルのような組合せ的な対象の個数と，数え上げ幾何学の答えが一致することがよく起こります．人間が理解できる重要な量は煎じ詰めればただの自然数ということはよくあります．自然数だからといって簡単というわけではないです．また，自然数を得る過程において，高次元のモジュライを駆使しますので，0 次元だけを扱っているわけではありません．

Q：どんな方法を使うのですか？
A：代数幾何学における交叉理論やトポロジーが基礎にあります．私がよく用いるのは特殊多項式の理論です．１９世紀に数え上げ幾何学が盛んに研究され始めた頃から，代数的な手法は用いられます．図形が満たす条件を代数的なシンボルとして扱って，答えを導きます．幾何学の問題が代数学に置き換わるところが面白いところです．

Q：特殊多項式とはなんですか？
A：多項式は知ってますよね．高校では整式と呼んでいます．一般には多変数の多項式を扱います．「特殊」というのは「とても個性的で性質が良い」というニュアンスです．代表例はシューア多項式と呼ばれる，多変数多項式の族です．さまざまな表示が可能で，互いの関係が具体的な公式によってよくわかる場合が多いです．さまざまな幾何学的な条件がそれと対応する特殊多項式によって見事に表されるのです．特殊多項式は表現論にも関係しています．

Q：表現論というのはなんですか？
A：自然科学において対称性の解明を目指すとき，線型表現の問題が重要になります．大ざっぱに言えば，線型代数学の拡張です．数学では対称性を「群」という抽象的な構造として理解します．「群」が自然界や数学の世界において行列の形で立ち現れてくる．これを線型表現といいます．上で述べた特殊多項式は表現の解明に用いられる「指標」という関数として解釈できることがあります．

Q：表現論を学ぶにはどうすればいいですか？
A：まずは線型代数学をしっかり勉強することです．数学科の2年生には「ベクトル空間と幾何」という講義で，線型代数の続編として表現論の入門を講義しています．来春にはこの講義内容をもとにした本「テンソル代数と表現論」を出版する予定です．

Q：数え上げ幾何学と表現論が関係するのはなぜですか？
A：どちらも群と深く結びついていますので，関係するのは自然ではあります．しかし，表面的な関係だけではなく，もっともっと深いところで繋がっていることが，ここ数年の研究の発展で徐々にわかっていました．さらにこの先の10年くらいで「数え上げ幾何学」がもっと面白くなるんではないかと思います．

笑いについての論考というのは案外少なく、今でも100年前の哲学者、ベルグソンの著作が重要な文献になっています。そこでは、繰り返すだけで笑いを起こす「反復」や、地位や役割の「反転」、一つの言葉や人物が両義的な意味を持つことに起因する「交錯」が、笑いを起こす３つのメカニズムとして挙げられています。しかし、これらの議論は、もはや古いギャグやダジャレの類だけを捉えているように思えます。もちろん現代の笑いにも通じるものはありますが、わかりやすい対立軸、例えば、ベルグソンの引用する主人と使用人のような対立軸はもはや明瞭ではなく、対立軸の浮かび上がること自体が、現代の笑いを形作っているように思えます。

研究室の学部生、神さんは、漫才が大好きでこれをなんとか卒論にできないかと相談してきました。日本には「カワイイ」や「マンザイ」の笑いなど、文化に独特のものがあり、それらはグロテスクさや不安、恐怖と紙一重です。それは創造のコアであるとも考えていましたので、すぐさま研究として立ち上げることにしました。桂枝雀は、笑いとは緊張の緩和であると言い、千原ジュニアは、ツッコミとは話を「フチドル」ことだと言っています。この二つは私の頭の中で繋がるものがありました。そこで神くんには、YouTubeに上がっている漫才を徹底的にみて文字に起こしてもらい、これらを調べることにしました。その結果、「フチドル」ということの意味が数理構造として可視化されると共に、緊張の緩和とも関係付けられることになりました。

典型的な事例は、フットボールアワーの次のようなネタに認められます。ボケである岩尾が、次のように話します。「そこを右に曲がるやろ、そうすると横断歩道がある」、「で、まっすぐ行って信号がある」、…、「そのまま行くと、S字クランクや」。と、ここでツッコミである後藤が叫びます。「それ、教習所やろ」。岩尾は、次々と新たな情報を加えていくだけですが、それは最後にはS字クランクとなり、街中の話かと思って聞いていた聴衆は、梯子をはずされたような不安に陥り緊張してしまう。それを後藤が、全て教習所の話だと説明しますから、聴衆はそれを聞いて緊張が解け、一気に爆笑が生じるわけです。バラバラな情報であった岩尾の話に意味を与えた「教習所」こそ、フチドリです。フチドリとは、図と地という対立軸を浮かび上がらせて意味を与え、緊張を緩和することと考えられます。

私たちは緊張の緩和を、「言葉の生起確率が、フチドリによって急に増大する」という形で、説明できると思いました。そこで、漫才における言葉の連なりを、発話とその意味に便宜上分けた後、両者の間の対称性を仮定し、これを二項関係（関係がある・ない）で表しました。ここから、言葉の可能な組み合わせが、漫才の流れ・分脈の中でどのように制限しているか、代数構造の一つである束（演算について閉じた順序集合）で表して解析しました。その結果、淡々と付加される情報の系列は、複数の対角関係（対角成分のみが関係を有する）の形をとり、フチドリは、対角関係の外側全てに関係を認め、文字通り対角関係を「縁取り」していることが分かりました。これを束で表すと、図のように対角関係はブール代数と呼ばれる集合論に対応する論理、フチドリは、それを貼り合わせる要素となることが分かりました。それは、量子論理と関係の深いオーソモジュラー束を部分とする形式で、様々な漫才のネタを解析すると、そのほとんどがこの形になっていることが分かりました。束上で主観的確率を定義すると、フチドリによって確率が上昇し、緊張の緩和を説明できることもわかりました。笑いは量子情報によって説明できるという議論が、一部でなされるようになりましたが、それを一部に含む、より普遍的な構造が笑いにはあるのかもしれません。

コンピュータで文章(テキスト)を扱う研究分野を自然言語処理と言います。「自然言語」と言っているのは、C言語やJava言語などのプログラミング言語と区別するためです。(しかし、最近では、プログラミング言語のコードの処理や自動生成に関する研究もありますので、単に「言語処理」でよいかもしれません。)

自然言語処理の研究の成果としては、検索エンジン、自動翻訳システムやチャットボットなどがあります。みなさんは、日頃、ウェブ上の検索エンジンを使って、調べたいことを検索しているのではないでしょうか。時には、自動翻訳システムで外国語を翻訳したり、スマートフォン上のチャットボットに質問することもあるかもしれません。

では、自然言語処理における難しさや問題はどこにあるのでしょうか? 次の3つが大きな問題として挙げられます。

・ことばの曖昧性
・知識の欠如
・文脈の適切な考慮

1つ目の問題の例として、「外国人参政権」の単語区切りの曖昧性を挙げます。

(1)
    a. 外国/人/参政/権
    b. 外国/人参/政権

日本語を知っている人であればaが正解だと容易に分かりますが、コンピュータには知識がないため分かりません。これが2つ目の知識の欠如の問題です。つまり、言語や世界に関する知識がコンピュータには欠如しているために、ことばを理解できないのです。

そこで、コンピュータに知識を与えることについて長い間研究されてきました。古くは人手で知識を与えていましたが、1990年代頃から、大量のテキストから自動的に獲得するという方法が主流になりました。さらに、ここ数年は深層学習が進展し、2018年に発表されたBERT [1]やその派生の深層学習モデルでは、テキスト中の単語を隠して、それを当てるという穴埋め問題を何度も繰り返し解くことで言語の基本的な知識を獲得しています(図参照)。このような穴埋め問題はテキストから自動的に大量に作り出せますので、人手をかけずに大量の学習データを作ることができるという利点があります。

3つ目の問題ですが、知識を用いて曖昧性を解消するには、文脈を適切に考慮する必要があります。次の2文では「米/原発」なのか「米原/発」なのかを文脈から判断しないといけません。

(2)
    a. 米原発、外部電源失い緊急停止
    b. 米原発の521系の列車の時刻

知識の獲得、および、獲得した知識の適切な利用によって、単語区切りの認識、構文構造の解析、同義語認識など多くの問題を高精度に解けるようになってきました。しかし、句や文の同義性の認識などはまだ難しく、ことばを本当に理解しているとは到底言えません。上記の知識獲得手法において、句や文のような大きな単位の穴埋め問題にする手法なども提案されていますが、まだ研究の真っ最中です。

テキストからの知識獲得手法にも限界があります。テキストに書いてあることは学習できても、書いていないことは学習できません。人は誰でも知っている常識的なことは基本的に書かず、むしろ変わったことやニュースを書く傾向があります。そのため、常識的な知識はクラウドソーシングなどで人に書いてもらって集合知として獲得するようなことが行われています。

我々の研究室では、コンピュータがテキストから自動的に獲得する知識と、集合知をうまく組み合わせて、ことばを真に理解する人工知能を作るべく、研究を進めています。今後ますます、検索エンジンや自動翻訳など、人の言語活動を支援するアプリケーションの精度が上がり、さらに便利になることが期待されます。

[1] Jacob Devlin, Ming-Wei Chang, Kenton Lee, and Kristina Toutanova. BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding. In Proc. of NAACL 2019, pp.4171–4186. https://aclanthology.org/N19-1423/